This is the final part of our series on entropy in machine learning. This post will focus on the differences between entropy and the Gini index, an alternative metric emerging as a computation-sparing entropy alternative.
What we cover in the article:
- Definition of the Gini index
- Key differences between entropy and the Gini index in machine learning
- Other concepts related to entropy: Relative entropy and cross-entropy
For an intuitive definition of the concept and practical examples of how it’s used to streamline decision trees, see Part 1 and Part 2, respectively.
What is the Gini index?
Entropy is a reliable way to measure the certainty of predictions an ML model yields, but it comes with a significant downside: it is computationally intensive.
To work around this problem, engineers typically use a more efficient metric: the Gini index.
Entropy needs more computational power than Gini impurity because it is a logarithmic function, which is more complex to calculate.
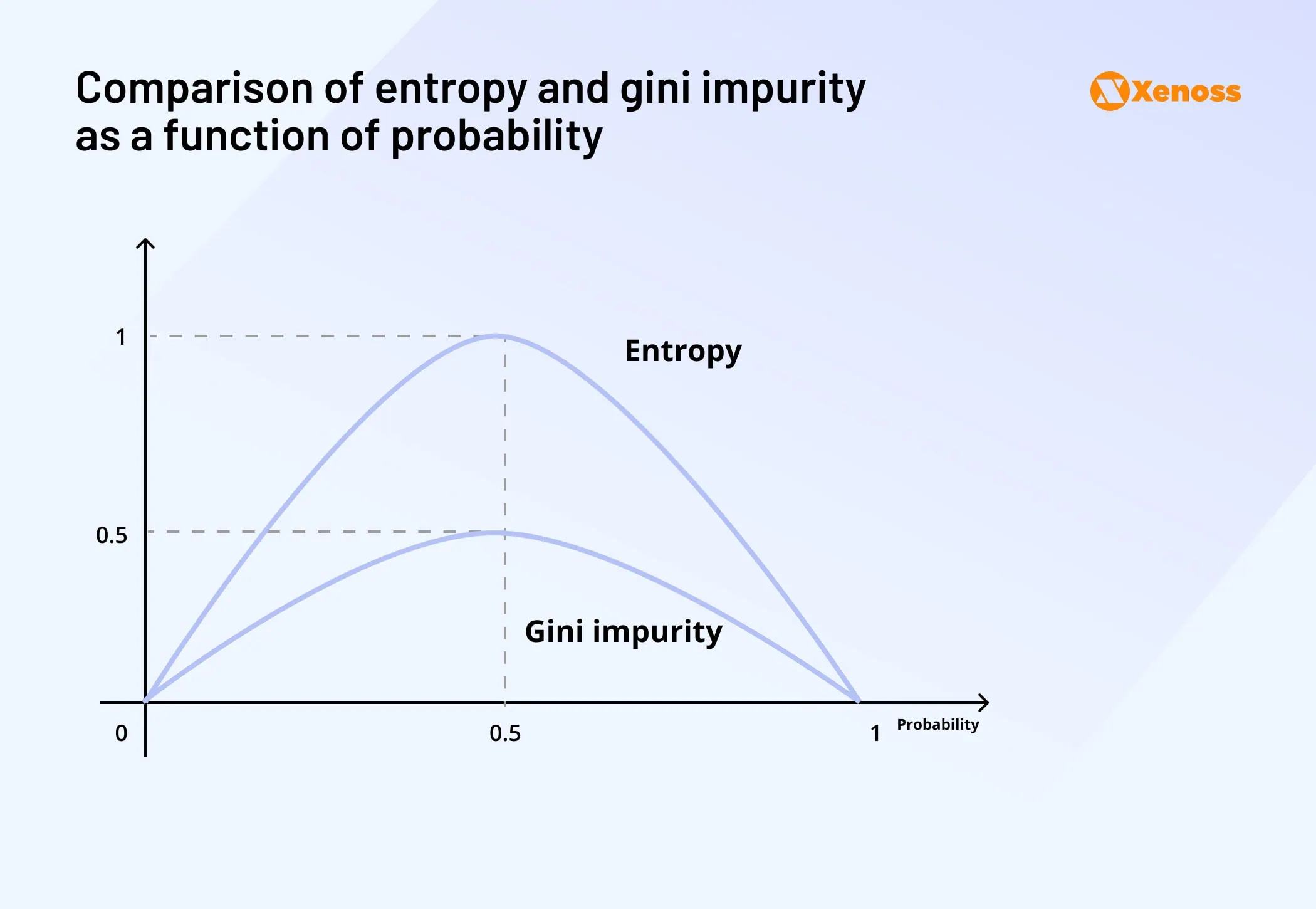
A different reason is that the highest plottable Entropy value is >1, whereas the highest possible Gini value is 0.5, as seen on the graph below.
A practical example of using the Gini index
Xenoss machine learning engineers used the Gini index to evaluate how well we improved the accuracy of credit scoring for a US bank expanding globally.
Optimizing the neural network architecture led to a +1.8 Gini point uplift.
Entropy vs Gini index: Summary of key differences
From an operational point of view, computational efficiency is the key difference between Gini and entropy. There are a few other distinctions, which we highlight in the table below.
| Difference | Gini Index | Entropy |
| Basic concept | Reflects how “impure” categories are | Reflects how “unpredictable” or “surprising” categories are |
| Ease of calculation | Generally quicker to compute (mostly simple counting) | Tends to be slower (involves a deeper look at “surprise” levels) |
| When it is used | Often chosen for decision trees due to speed and simplicity | Commonly used where more detailed insight into uncertainty is desired |
| Speed | Slightly faster for large datasets; good “quick check” | Provides a more nuanced measure of information but takes longer |
Concepts related to entropy in machine learning
Cross-entropy loss
After a model generates a range of predictions, a machine learning engineer can match them against real-world outcomes and reward the model for making correct assumptions.
After comparing estimates and outcomes, engineers might get a graph similar to this one.
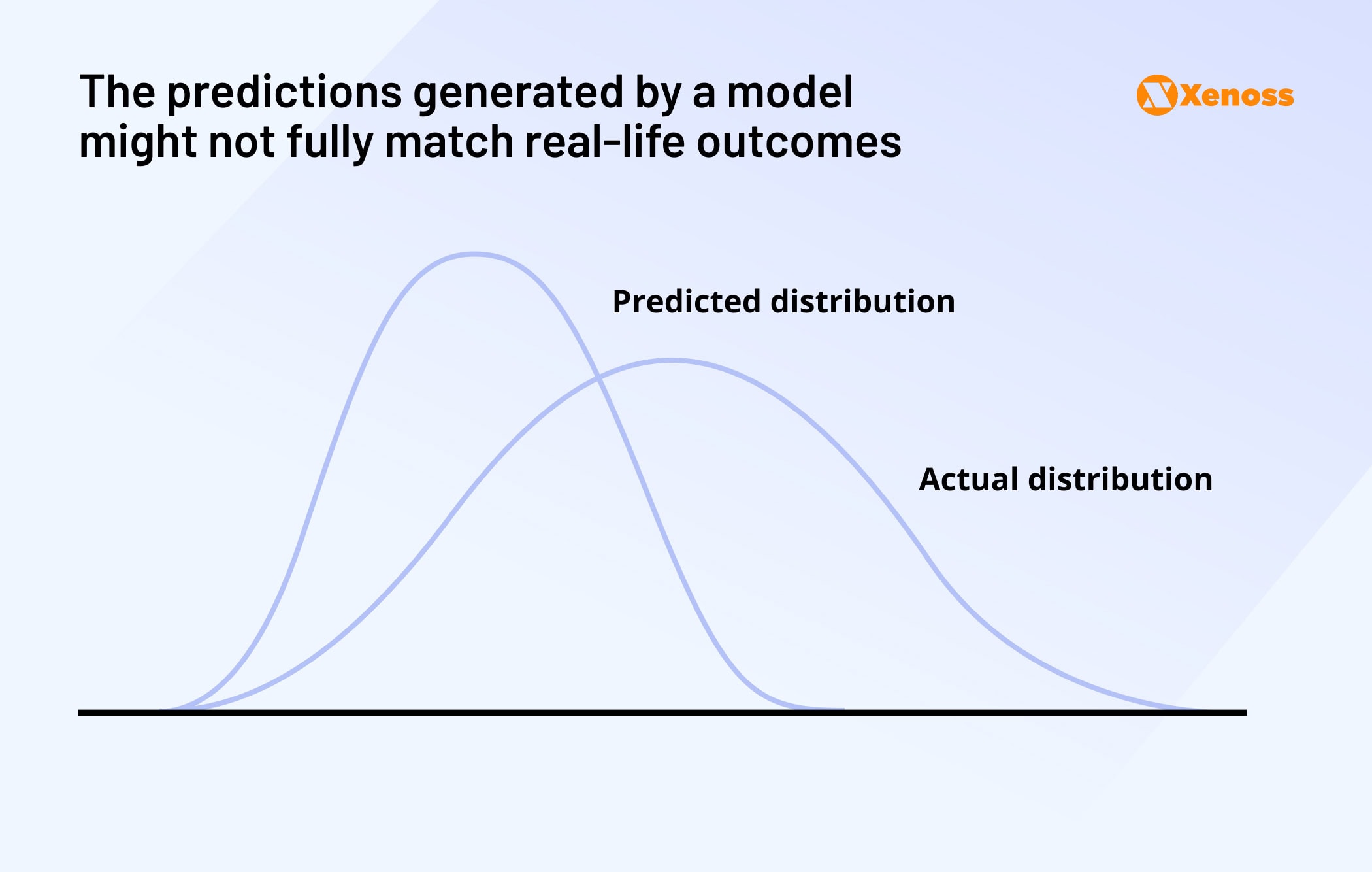
ML developers use cross-entropy loss to quantify this visual representation and understand how well a model handles predicting accurate outcomes.
The entropy loss between the model’s output and real-world data is minimal in more confident models. In contrast, cross-entropy loss will increase if the model confidently predicts the wrong outcome.
A simple example will help get a clear idea of how ML teams use cross-entropy loss.
Example: Cat or dog?
Imagine you designed a simple model that needs to classify pets in photos as “cats” or “dogs”.
You show your model a photo, and it predicts:
- There’s a 70% chance it is a “cat”.
- 30% chance it is a “dog”.
Let’s assume the picture you showed was that of a “cat.”
Cross-entropy loss will compare the model’s predicted probability distribution (70% cat, 30% dog) to the accurate distribution (100% cat, 0% dog). It then calculates a measure of “how far off” the prediction is from the truth.
- If your model is correct and confident (e.g., it predicts 95% cat for an actual cat), the cross-entropy loss will be a small number (meaning “good job”).
- If your model is wrong or uncertain (e.g., predicts 10% cat for an actual cat), the cross-entropy loss will be significant (meaning “improve your predictions”)
In other words, cross-entropy loss penalizes your model for being wrong and rewards it for being both correct and confident.
By repeating this process across many examples—cats, dogs, and maybe other animals—your model learns to adjust its internal parameters so that its predicted probabilities match the true answers more closely.
Relative entropy
To avoid the need for a mathematical model, relative entropy can be considered as the change in uncertainty about a variable when it yields a new probability distribution.
This likely sounds like a mouthful, so let’s return to the coin toss experiment to grasp the concept better.
A regular coin has an equal probability (p = 0.5) of landing either heads or tails. However, suppose a trusted friend tells you that the coin has been tampered with in such a way to favor heads strongly. In this case, you will have an 80% chance (p = 0.8) to get Heads every time you flip.
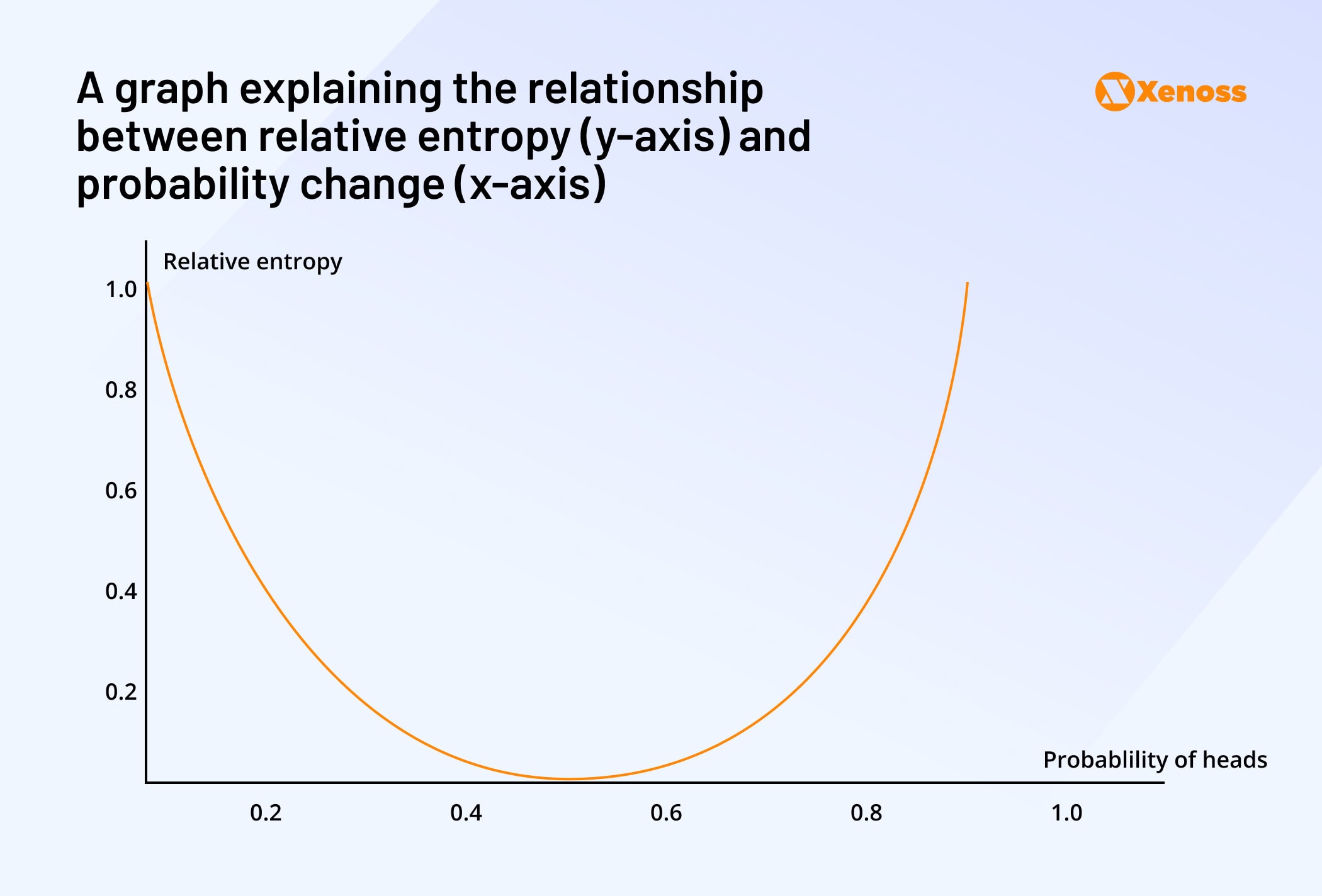
A change between the entropy and the probabilities of both events is relative entropy.
Plotting this graphically, you can notice that relative entropy is highest when all uncertainty has been eliminated.
Why is relative entropy functional?
Like cross-entropy (the two are related as the difference between entropy and cross-entropy loss is, in fact, relative entropy), it allows an understanding of how different the model’s outputs are from reality.
Machine learning engineers should strive to reduce the relative entropy of their predictions.
The bottom line
Since entropy is still a commonplace metric for assessing the performance of machine learning models, non-technical decision-makers in AI products would find it helpful to have a solid idea of the concept.
Inaccurate models do not just fail to generate value but actively harm organizational decision-making.
That is why running regular entropy calculations is helpful to ensure your ML algorithms are in touch with real-world trends and drive the value organizations hope to derive from machine learning projects.